Numpy以外のコンテナ
Python では,値の集合を「コンテナ」と呼び,代表的なものとして
リスト(List): [1, 'two', [3], 3.14]
タプル(Tuple): (1, 'two', [3], 3.14)
文字列(Str): 'aa83988848'
集合(Set): {1, 'two', [3], 3.14}
辞書(Dict): {'v1':1, 'v2':'two', 'v3':[3], 'v4':3.14}
があります.コンテナは,基本的に各要素が異なる型(クラス)でも構いません.要素がさらにコンテナであっても構いません.
= [1 , 'two' , [3 ], 3.14 ]= (1 , 'two' , [3 ], 3.14 )= 'aa83988848' = {1 , 'two' , 3.14 } # setはコンテナを要素に持てない = {'v1' :1 , 'v2' :'two' , 'v3' :[3 ], 'v4' :3.14 }print ('==MyList==' )print (f' { MyList} \n ' )print ('==MyTuple==' )print (f' { MyTuple} \n ' )print ('==MyStr==' )print (f' { MyStr} \n ' )print ('==MySet==' )print (f' { MySet} \n ' )print ('==MyDict==' )print (f' { MyDict} \n ' )
==MyList==
[1, 'two', [3], 3.14]
==MyTuple==
(1, 'two', [3], 3.14)
==MyStr==
aa83988848
==MySet==
{'two', 1, 3.14}
==MyDict==
{'v1': 1, 'v2': 'two', 'v3': [3], 'v4': 3.14}
Numpy以外のコンテナに対する演算
これらのコンテナに対して演算をすると
print ("==MyList * 3==" )print (f" { MyList * 3 } \n " )print ("==MyTuple * 3==" )print (f" { MyTuple * 3 } \n " )print ("==MyStr * 3==" )print (f" { MyStr * 3 } \n " )# print('==MySet * 3==') # print(f'{MySet * 3}\n') # Setは演算できない # print('==MyDict * 3==') # print(f'{MyDict * 3}'\n) # Dictは演算できない = [1 , 2 , 3 ]print ("==MyList + MyList2==" )print (f" { MyList + MyList2} \n " )
==MyList * 3==
[1, 'two', [3], 3.14, 1, 'two', [3], 3.14, 1, 'two', [3], 3.14]
==MyTuple * 3==
(1, 'two', [3], 3.14, 1, 'two', [3], 3.14, 1, 'two', [3], 3.14)
==MyStr * 3==
aa83988848aa83988848aa83988848
==MyList + MyList2==
[1, 'two', [3], 3.14, 1, 2, 3]
というように,後ろに繰り返し要素を付け加えることになります.
numpy.NDarray はベクトル演算それぞれの要素に対し演算するには,どうしたらいいでしょうか.そのような演算をベクトル演算といいます.
ベクトル演算をするためのコンテナを Numpy NDArray といいます.
NumPy というパッケージに NumPy NDArray クラスが定義されています.
import numpy as np= [2 , 3 , 5 ,7 ]print ('==MyList==' )print (f' { MyList} \n ' )print ('==MyList * 3==' )print (f' { MyList * 3 } \n ' )= np.array(MyList) # <-- Numpy NDArray print ('==MyArray==' )print (f' { MyArray} \n ' )print ('==MyArray * 3==' )print (f' { MyArray * 3 } \n ' )
==MyList==
[2, 3, 5, 7]
==MyList * 3==
[2, 3, 5, 7, 2, 3, 5, 7, 2, 3, 5, 7]
==MyArray==
[2 3 5 7]
==MyArray * 3==
[ 6 9 15 21]
要素数の異なる NumpyArray との加算はできません.
= np.array(MyList2)print (f" { MyArray + MyArray2} " )
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[4] , line 2
1 MyArray2 = np.array(MyList2)
----> 2 print (f " { MyArray + MyArray2 } " )
ValueError : operands could not be broadcast together with shapes (4,) (3,)
NumpyArray は,線形代数における行列やベクトルなので,行列やベクトルに対する演算しか許されないというわけです.
numpy.NDArray は本当はテンソル演算「NumpyArray は,行列やベクトル」と言いましたが,行列やベクトルには形があります.
\[
\pmb{M} = \begin{bmatrix}
1 & 2 & 3\\
4 & 5 & 6
\end{bmatrix}
\]
のとき,\(\pmb{M}\) の形は「2 行 3 列」です.
\[
\pmb{v} = \begin{bmatrix}
7\\
8\\
9
\end{bmatrix}
\]
のとき,\(\pmb{v}\) の形は「3 行 1 列」ですね.
\[
\pmb{u} = \begin{bmatrix} 10 & 11\end{bmatrix}
\]
のとき,\(\pmb{u}\) の形は「1 行 2 列」ですね.
NumpyArray で 2 行 3 列の行列を作ってみましょう. すべての要素がゼロな 2 行 3 列の行列は,NumPy の zeros 関数で作ることができます.
= np.zeros((2 ,3 ))print (f' { M = } ' )
M = array([[0., 0., 0.],
[0., 0., 0.]])
行列の形は 属性.shapeに保存されています.
形 (2,3) の M をprintしたときの表示を見てみると,「行ごとの 3 つの要素がリストになっており,2 行のリストをさらにリストに」しています.
実は,このような リストから NumpyArray を作る こともできます.
= [1 ,2 ,3 ]= [4 ,5 ,6 ]= [u1, u2]= np.array(L)print (f' { M = } ' )print (f' { M. shape = } ' )
M = array([[1, 2, 3],
[4, 5, 6]])
M.shape = (2, 3)
では,7 と 8 と 9 を要素にもつ 1 行 3 列の NumpyArray を作ってみましょう.行ごとにリストに,全体をさらにリストにします.つまり 2 重リストになります.
= [[7 ,8 ,9 ]]= np.array(Lx)print (f' { x = } ' )print (f' { x. shape = } ' )
x = array([[7, 8, 9]])
x.shape = (1, 3)
この x を転置した \(\pmb{x^{\prime}}\) ならば,\(\pmb{M}\pmb{x^{\prime}}\) が計算できます.転置は Numpy の transpose 関数を使います.また,行列積は Numpy の matmul 関数です.(ちなみに 演算子 * は,要素積(要素同士の積) です.)
= np.transpose(x)# `x_prime = x.T` でもよい. = np.matmul(M, x_prime)print (f" { R = } " )print (f" { R. shape = } " )
R = array([[ 50],
[122]])
R.shape = (2, 1)
皆が知っているように,行列積は,「左の行列の列数」と「右の行列の行数」が同じでなければいけません.上の例の場合,shapeが (2,3) と (3,1) なので行列積の shape は (2,1) となるわけですね.
ところで,
この x は行列でしょうか?ベクトルでしょうか?
行ベクトルとか列ベクトルと言われているものですが,Numpy では 「行数」とか「列数」とか言っているので,これは「行列」なのです.shapeが 2元タプルになっています.
先の x が行列ならば,ベクトルはどんなもの?
ベクトルとは,1 重のリストから作ったもの をいいます. 「行」や「列」という概念がありません.
= [7 ,8 ,9 ]= np.array(Ly)print (f' { y = } ' )print (f' { y. shape = } ' )
y = array([7, 8, 9])
y.shape = (3,)
さきほどの行ベクトル(\(\in\) 行列) x は shape が (1,3) で,転置した np.transpose(x) は (3,1) で 列ベクトルでした. 今度のベクトル y は shape が (3,) です.2元目がヌル(空)で,1元タプルです.
ちなみに,行や列の概念が無いので転置は無意味で,形を変えません.
print (f" { y. T = } " )print (f" { y. T. shape = } " )
y.T = array([7, 8, 9])
y.T.shape = (3,)
さきほどの行列積ができます.ベクトルは行列に右から掛けます.
= np.matmul(M, y)print (f' { R2 = } ' )print (f' { R2. shape = } ' )
R2 = array([ 50, 122])
R2.shape = (2,)
R2 はさきほどの R と要素は同じ数値ですが,shape が (2,1) ではなく (2,) となります.(行列積の作られ方どおりです.)
ちなみに,内積というのもありました.\(a\) も \(b\) も行列ならば \(a^\top b\) で計算されるので,np.matmul(a.T, b) です.
ところで Numpy にも内積は用意されていて, np.inner(a,b) です.しかし,a と b が行列のとき,\(a^{\top}b\) にはなりません. 本来の内積の定義は,「内側の積和」であり,\(\sum_{i=1}^{N} \pmb{a_i} \pmb{b_i}\) という演算です(\(N\) は \(R-1\) 階の次数.\(R\) は階数)
= np.array([[1 ], [2 ]])= np.array([1 , 2 ])= np.array([[3 ], [4 ]])= np.array([3 , 4 ])= np.inner(vc1, vc2)print (f" { inner1 = } " )= np.matmul(vc1.T, vc2)print (f" { inner2 = } " )= np.inner(v1, v2)print (f" { inner3 = } " )
inner1 = array([[3, 4],
[6, 8]])
inner2 = array([[11]])
inner3 = 11
まとめると
行列: 2 重のリストから作られる.形は (S1, S2),行数 S1, 列数 S2
ベクトル: 1 重のリストから作られる.形は (S1,), 要素数 S1
行列積は,np.matmul 関数で,
左の Array の形が(S1,S2)で,右の Array の形が(S3,S4)のとき,S2==S3 なら演算できて,答えの Array の形は(S1,S4)
転置は np.transpose 関数で,
形が(S1,S2)の行列の転置は,形が(S2,S1)となる
形が(S1,)のベクトルの転置は,形が変わらず(S1,)となる
print (y.shape)= np.transpose(y)print (yt.shape)
テンソル
行列やベクトルをまとめて,一般的に「テンソル」と言います.
さきほどの「n 重のリスト」の n を階数といいます.
行列: 2 階テンソル
ベクトル: 1 階テンソル
ここで,1 重リストを並べたものをさらにリストにすれば,2 重リストになるので,すなわち(S1,)ベクトル(1 階テンソル)を S2 個並べると(S2,S1)行列(2 階テンソル)になるということです. 要素が(S1,)ベクトルである(S2,)ベクトルは,(S2,S1)という行列になります.
属性.ndimに保存されています.属性.shapeに保存されている「形」を表すタプルの要素数でもあります.
= np.array([1 ,2 ,3 ,4 ])print (A1)print (f'shape(形): { A1. shape} ' )print (f'ndim(階数): { A1. ndim} ' )print (f'size(要素数): { A1. size} ' )print (' \n ' )= np.array([[1 ,2 ,3 ,4 ]])print (A2)print (f'shape(形): { A2. shape} ' )print (f'ndim(階数): { A2. ndim} ' )print (f'size(要素数): { A2. size} ' )print (' \n ' )= np.array([[[1 ,2 ,3 ,4 ]]])print (A2)print (f'shape(形): { A3. shape} ' )print (f'ndim(階数): { A3. ndim} ' )print (f'size(要素数): { A3. size} ' )print (' \n ' )
[1 2 3 4]
shape(形):(4,)
ndim(階数):1
size(要素数):4
[[1 2 3 4]]
shape(形):(1, 4)
ndim(階数):2
size(要素数):4
[[1 2 3 4]]
shape(形):(1, 1, 4)
ndim(階数):3
size(要素数):4
3 階以上になっても行列積(テンソル積)は同じです.
= np.array([[[1 ,2 ,3 ,4 ]]])= np.array([5 ,6 ,7 ,8 ])= np.matmul(T3,T1)print (f' { T3. ndim} 階テンソル(形 { T3. shape} )と { T1. ndim} 階テンソル(形 { T1. shape} )の行列積は { Result. ndim} 階テンソル(形 { Result. shape} )' )print (Result)
3階テンソル(形(1, 1, 4))と1階テンソル(形(4,))の行列積は2階テンソル(形(1, 1))
[[70]]
抽出
= np.array([[1 ,2 ,3 ,4 ],[5 ,6 ,7 ,8 ],[9 ,10 ,11 ,12 ]])print (M,type (M),M.shape,M.ndim,M.size,' \n ' )= M[1 ] # 行 print (M_row,type (M_row),M_row.shape,M_row.ndim,M_row.size,' \n ' )= M[1 ][2 ] # (1,2)要素 M[1,2]とは書けない print (M_item,type (M_item),M_item.shape,M_item.ndim,M_item.size,' \n ' )= M[1 :3 , 0 :2 ] #スライス print (M_slice,type (M_slice),M_slice.shape,M_slice.ndim,M_slice.size,' \n ' )= M[:, 1 ] # 列抽出はスライスで print (M_column,type (M_column),M_column.shape,M_column.ndim,M_column.size,' \n ' )= M[[0 ,2 ],[1 ,3 ]] # (0,1)要素と(2,3)要素 (スライス) print (M_sub,type (M_sub),M_sub.shape,M_sub.ndim,M_sub.size)
[[ 1 2 3 4]
[ 5 6 7 8]
[ 9 10 11 12]] <class 'numpy.ndarray'> (3, 4) 2 12
[5 6 7 8] <class 'numpy.ndarray'> (4,) 1 4
7 <class 'numpy.int64'> () 0 1
[[ 5 6]
[ 9 10]] <class 'numpy.ndarray'> (2, 2) 2 4
[ 2 6 10] <class 'numpy.ndarray'> (3,) 1 3
[ 2 12] <class 'numpy.ndarray'> (2,) 1 2
追加
= np.array([[1 ,2 ],[3 ,4 ]])= np.array([[11 ,12 ],[13 ,14 ]])print ('==np.concat: 階数を変えずに,連結する.==' )= np.concatenate([u1,u2])print (M1)print (f'形: { M1. shape} ,階: { M1. ndim} ,要素数: { M1. size} \n ' )= np.concatenate([u1,u2],axis= 1 )print (M2)print (f'形: { M2. shape} ,階: { M2. ndim} ,要素数: { M2. size} \n ' )print ('==np.stack: 指定した階に,積む==' )= np.stack([u1,u2],axis= 0 )print (M3)print (f'形: { M3. shape} ,階: { M3. ndim} ,要素数: { M3. size} \n ' )= np.stack([u1,u2],axis= 1 )print (M4)print (f'形: { M4. shape} ,階: { M4. ndim} ,要素数: { M4. size} \n ' )= np.stack([u1,u2],axis= 2 )print (M5)print (f'形: { M5. shape} ,階: { M5. ndim} ,要素数: { M5. size} \n ' )
==np.concat: 階数を変えずに,連結する.==
[[ 1 2]
[ 3 4]
[11 12]
[13 14]]
形:(4, 2),階:2,要素数:8
[[ 1 2 11 12]
[ 3 4 13 14]]
形:(2, 4),階:2,要素数:8
==np.stack: 指定した階に,積む==
[[[ 1 2]
[ 3 4]]
[[11 12]
[13 14]]]
形:(2, 2, 2),階:3,要素数:8
[[[ 1 2]
[11 12]]
[[ 3 4]
[13 14]]]
形:(2, 2, 2),階:3,要素数:8
[[[ 1 11]
[ 2 12]]
[[ 3 13]
[ 4 14]]]
形:(2, 2, 2),階:3,要素数:8
形を変形
= np.array([[1 ,2 ,3 ,4 ],[5 ,6 ,7 ,8 ]])print (T)print (f'形: { T. shape} , 階: { T. ndim} , 要素数: { T. size} \n ' )= np.reshape(T,(1 ,8 ))print (T2)print ('前から順に8要素のリストを1個' )print (f'形: { T2. shape} , 階: { T2. ndim} , 要素数: { T2. size} \n ' )= np.reshape(T,(8 ,1 ))print (T3)print ('前から順に1要素のリストを8個' )print (f'形: { T3. shape} , 階: { T3. ndim} , 要素数: { T3. size} \n ' )= np.reshape(T,(4 ,2 ))print (T4)print ('前から順に2要素のリストを4個' )print (f'形: { T4. shape} , 階: { T4. ndim} , 要素数: { T4. size} \n ' )= np.reshape(T,(8 ,))print (T5)print ('前から順に8要素' )print (f'形: { T5. shape} , 階: { T5. ndim} , 要素数: { T5. size} \n ' )= np.reshape(T,(1 ,2 ,4 ))print (T6)print ('前から順に4要素2個の要素を1個' )print (f'形: { T6. shape} , 階: { T6. ndim} , 要素数: { T6. size} \n ' )
[[1 2 3 4]
[5 6 7 8]]
形:(2, 4), 階:2, 要素数:8
[[1 2 3 4 5 6 7 8]]
前から順に8要素のリストを1個
形:(1, 8), 階:2, 要素数:8
[[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]]
前から順に1要素のリストを8個
形:(8, 1), 階:2, 要素数:8
[[1 2]
[3 4]
[5 6]
[7 8]]
前から順に2要素のリストを4個
形:(4, 2), 階:2, 要素数:8
[1 2 3 4 5 6 7 8]
前から順に8要素
形:(8,), 階:1, 要素数:8
[[[1 2 3 4]
[5 6 7 8]]]
前から順に4要素2個の要素を1個
形:(1, 2, 4), 階:3, 要素数:8
pandas のデータフレーム
行列といえば,データフレームと見た目が似ています.
どちらも,行の要素数が各列で同じ,列の要素数が各行で同じでなければならない.(普通の List,Tuple,Set,Dict では違う)
ということで,
2 階テンソル(行列)の NumpyArray は pandas データフレームに変換できます.: pandas のDataFrame関数
pandas データフレームは,2 階の NumpyArray(行列)に変換できます.: pandas の DataFrame クラスのto_numpyメソッド
NumpyArray の行が,pandas の 1 行のサンプルに対応しています.
import pandas as pd= np.array([[1 , 2 , 3 , 4 ], [5 , 6 , 7 , 8 ], [9 , 10 , 11 , 12 ]])= ["v0" , "v1" , "v2" , "v3" ]= ["#1" , "#2" , "#3" ]= pd.DataFrame(M, columns= columnsM, index= indexM)# dataframe to numpy ndarray = df.to_numpy()
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
#1
1
2
3
4
#2
5
6
7
8
#3
9
10
11
12
array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12]])
pandas.read_html によるスクレイピング
ホームページや画像などからデータフレームを読み込む操作を「スクレイピング」と呼びます.
例えば,長崎の気温変化をデータフレームに読み込んでみましょう.
長崎の気温変化は,Link にあります.
このページには,文章の中に,表がありますね.
pandas のread_html関数は URL を指定すると,その URL のページに含まれる表の数だけデータフレームを作って,そのリストを返します. (html/xml を解釈する外部パッケージ lxml のインストールが必要です.)
python コードによるスクレイピングは,機械的な自動操作なのでホームページ作成者から敬遠される傾向があります. もし python コードから https 経由でファイルを読み込めない場合は,普段使っているウェブブラウザで手動で読み込み,ページをstats_nagasaki.htmlなどと名前をつけて保存し, それを読み込むように変更してください.
import lxmlfrom datetime import datetime= "https://www.data.jma.go.jp/obd/stats/etrn/view/monthly_s3.php?prec_no=84&block_no=47817&year=&month=&day=&view=a1" # URL = "stats_nagasaki.html" = pd.read_html(URL, header= 0 )= df_List[0 ]
0
1878
NaN
NaN
NaN
NaN
NaN
NaN
26.0
26.6
24.9
19.2
12.1
6.9
19.3 ]
1
1879
5.7
7.7
8.8
14.2
18.6
21.9
26.6
27.6
23.3
17.2
12.1
8.4
16.0
2
1880
4.8
8.3
9.9
14.1
19.4
21.2
25.4
25.8
23.7
18.8
11.7
5.3
15.7
3
1881
4.0
5.9
7.5
14.1
18.8
22.3
26.3
27.8
24.6
18.2
13.6
7.9
15.9
4
1882
7.3
6.7
8.8
14.7
17.9
20.6
25.0
26.4
23.0
19.4
12.3
6.8
15.7
...
...
...
...
...
...
...
...
...
...
...
...
...
...
...
143
2021
7.4
10.3
13.9
16.7
19.8
23.7
27.9
27.3
25.7
21.1
14.1
9.2
18.1
144
2022
7.1
6.5
12.9
16.4
20.0
23.9
27.8
28.6
25.9
19.9
16.5
7.8
17.8
145
2023
7.4
9.2
13.6
16.9
19.7
23.7
28.0
29.2
26.7
19.8
15.1
10.2
18.3
146
2024
8.4
10.6
12.0
17.7
20.0
23.2
28.4
29.8
28.6
22.6
16.5
9.0
18.9
147
2025
6.9
5.8
12.1
16.1
19.4
21.1 ]
NaN
NaN
NaN
NaN
NaN
NaN
12.1 ]
148 rows × 14 columns
「年の値」の列は,その年の平均気温です.今回は使わないので消します.
各月の値は,すべて同じ尺度・分布になっていて,いわゆるwide形式 なので,メルトでlong形式に直します. 列「年」を固定して,その他の列について,その列名を変数に,値を変数の値に整形します. - id_vars = ["年"] - var_name = '月' # 元の列名を 列「月」の値にする. -value_name = ‘気温’ # 元の列の値を 列「気温」の値にする.
= df.drop(columns= '年の値' )= df.melt(id_vars= ["年" ], var_name= '月' , value_name= '気温' ) # pd.melt() : 先週やった pivotの逆操作
0
1878
1月
NaN
1
1879
1月
5.7
2
1880
1月
4.8
3
1881
1月
4.0
4
1882
1月
7.3
...
...
...
...
1771
2021
12月
9.2
1772
2022
12月
7.8
1773
2023
12月
10.2
1774
2024
12月
9.0
1775
2025
12月
NaN
1776 rows × 3 columns
列「年」の値(例えば「1920」)と 列「月」を値(例えば「4月」)を合成すると,1つの列「年月」の値としてまとめることができます.
"年月" ] = df2["年" ].astype(str ) + "年" + df2["月" ].astype(str )
0
1878
1月
NaN
1878年1月
1
1879
1月
5.7
1879年1月
2
1880
1月
4.8
1880年1月
3
1881
1月
4.0
1881年1月
4
1882
1月
7.3
1882年1月
...
...
...
...
...
1771
2021
12月
9.2
2021年12月
1772
2022
12月
7.8
2022年12月
1773
2023
12月
10.2
2023年12月
1774
2024
12月
9.0
2024年12月
1775
2025
12月
NaN
2025年12月
1776 rows × 4 columns
列「年月」は,時刻データとして扱うようにします.
'Date' ] = [datetime.strptime(s,'%Y年%m月' ) for s in df2['年月' ]]
0
1878
1月
NaN
1878年1月
1878-01-01
1
1879
1月
5.7
1879年1月
1879-01-01
2
1880
1月
4.8
1880年1月
1880-01-01
3
1881
1月
4.0
1881年1月
1881-01-01
4
1882
1月
7.3
1882年1月
1882-01-01
...
...
...
...
...
...
1771
2021
12月
9.2
2021年12月
2021-12-01
1772
2022
12月
7.8
2022年12月
2022-12-01
1773
2023
12月
10.2
2023年12月
2023-12-01
1774
2024
12月
9.0
2024年12月
2024-12-01
1775
2025
12月
NaN
2025年12月
2025-12-01
1776 rows × 5 columns
整形前の列は,もう不要なので消します.
= df2.drop(columns= ['年' ,'月' ,'年月' ])
0
NaN
1878-01-01
1
5.7
1879-01-01
2
4.8
1880-01-01
3
4.0
1881-01-01
4
7.3
1882-01-01
...
...
...
1771
9.2
2021-12-01
1772
7.8
2022-12-01
1773
10.2
2023-12-01
1774
9.0
2024-12-01
1775
NaN
2025-12-01
1776 rows × 2 columns
列「気温」の値は間隔尺度なので,floatにしたいのですが, 数字以外の記号が含まれているので,まずその記号部分を消します.
'気温' ] = df3['気温' ].astype(str )'気温' ] = df3['気温' ].str .extract('([ 0-9.]+)' ) # 「0」~「9」,「.」で構成される文字列(すなわち気温の数値)を取り出す. "気温" ] = df3["気温" ].astype(float )
0
NaN
1878-01-01
1
5.7
1879-01-01
2
4.8
1880-01-01
3
4.0
1881-01-01
4
7.3
1882-01-01
...
...
...
1771
9.2
2021-12-01
1772
7.8
2022-12-01
1773
10.2
2023-12-01
1774
9.0
2024-12-01
1775
NaN
2025-12-01
1776 rows × 2 columns
NaN は,Not-A-Number(非数)を表します.欠損値ですので,気温がNaNの行は測定されていないことを表します.このような行を消します.
1
5.7
1879-01-01
2
4.8
1880-01-01
3
4.0
1881-01-01
4
7.3
1882-01-01
5
5.8
1883-01-01
...
...
...
1770
8.5
2020-12-01
1771
9.2
2021-12-01
1772
7.8
2022-12-01
1773
10.2
2023-12-01
1774
9.0
2024-12-01
1763 rows × 2 columns
Date列をインデックスにして昇順に並べ直します.
= df4.set_index("Date" )= df5.sort_index()= df5.reset_index('Date' )
0
1878-07-01
26.0
1
1878-08-01
26.6
2
1878-09-01
24.9
3
1878-10-01
19.2
4
1878-11-01
12.1
...
...
...
1758
2025-02-01
5.8
1759
2025-03-01
12.1
1760
2025-04-01
16.1
1761
2025-05-01
19.4
1762
2025-06-01
21.1
1763 rows × 2 columns
matplotlib
Matplotlib は,入力した系列に対応してグラフを描くライブラリです.
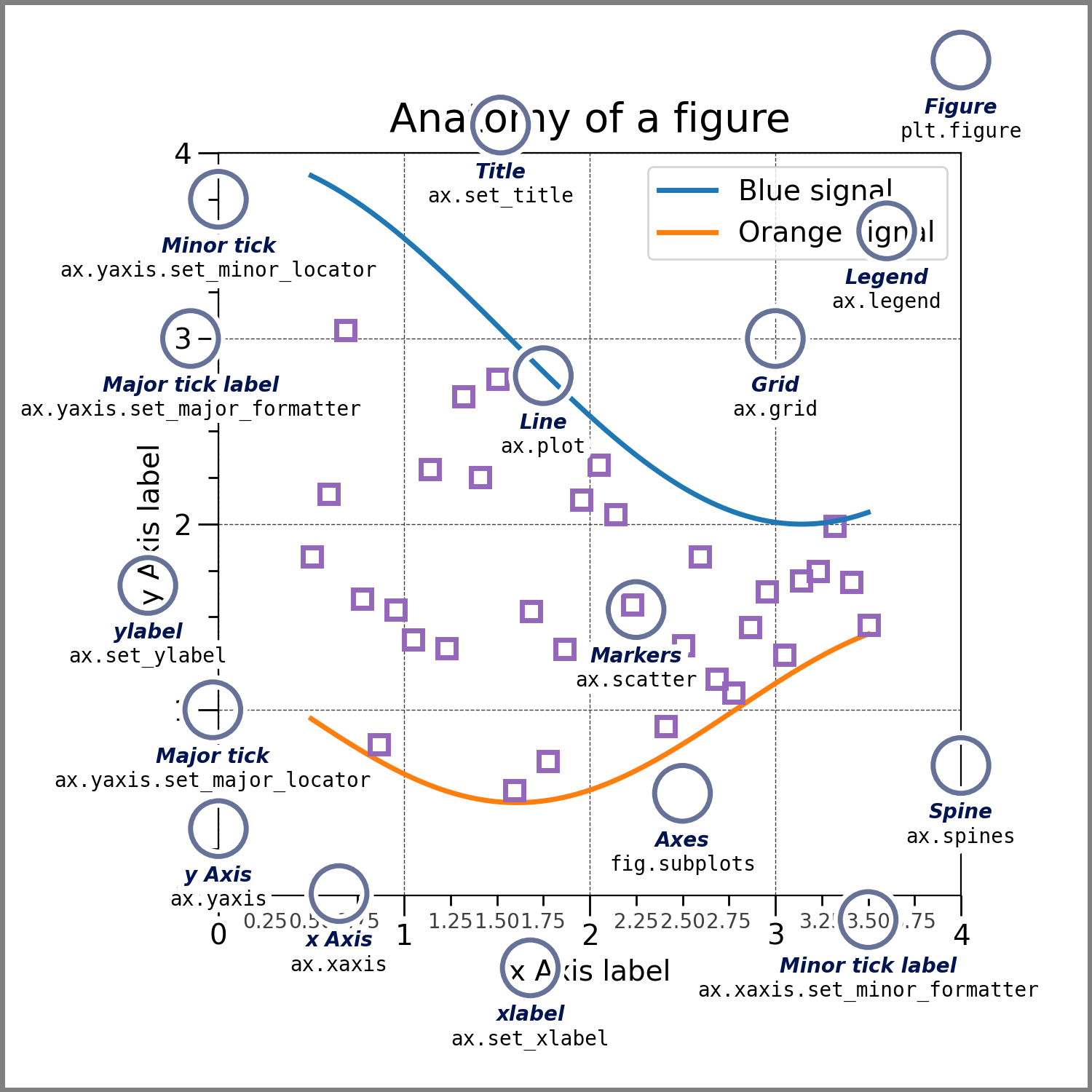
下のようなグラフを描きます.このグラフに書いてある用語(英単語)をそのまま覚えてください.
Figure:フィギュア:所謂,キャンバスのことです.Figure に描かれるのは,
複数のグラフ(Axes)
キャンバスのタイトル,凡例
Axes:アクセス:所謂,グラフのことです.Axes に描かれるのは,
軸線(Axis)
軸ラベル(xlabel, ylabel)
プロット(Plot, データを使って書かれた線や点)
Axis:アクシス:所謂,軸線のことです.Axis 上に描かれるのは,
目盛印(Tick,ティック):目盛として軸に刻みで描かれる細い線
目盛文字列(Tick Label):目盛の刻みに振られる文字列(数直線ならば数字.数字でなくてもいい)
グラフを描くには,
まず,キャンバスを用意する
from matplotlib import pyplot as plt= plt.figure(figsize= (10 , 5 ), tight_layout= True )
<Figure size 960x480 with 0 Axes>
<Figure size 960x480 with 0 Axes>
グラフ領域を用意する: fig.add_subplot(3,2,4)
例) キャンバスを 3 行 2 列の行列状に領域を分けたときの左上から 4 番目の領域
# グラフ領域を用意 # 例えばキャンバスを 2x3 に分割し,左上から右下に横方向に数えて,1番目と5番目に作成 = fig.add_subplot(2 ,3 ,1 )= fig.add_subplot(2 ,3 ,5 )
グラフを描く
2.1. プロットを描く
```
ax1.plot(x座標の系列, y座標の系列)
```
# 2024年の全ての月を抽出 `df[]` の中は,target_yearの1月1日以上,かつ, # target_yearの翌年1月1日より小さい を満たすような日付を # df5の列["Date"]から探したときの,その行番号のリストとなります. = 2024 = df5[1 , 1 ) <= df5["Date" ])& (df5["Date" ] < datetime(target_year + 1 , 1 , 1 ))# 内包表記. # df6の列["Date"]の値の全てをリストとして,その要素をfor文でいちいち抽出するという操作でリストを作る. = [dt.month for dt in df6["Date" ]]"気温" ])
2.2. 軸ラベル,タイトル,凡例を補正する
```
ax1.set_xlabel('横軸ラベル')
```
"Month" )"temperature" )f"Nagasaki { target_year} " )
2.3. グリッド線をつけたり,表示領域を決めたり
```
ax1.set_xlim()
ax1.grid()
```
0 ,35 ])1 ,12 ])
キャンバスの別の領域に別のグラフを書く
= 1879 = df5[1 , 1 ) <= df5["Date" ])& (df5["Date" ] < datetime(target_year2 + 1 , 1 , 1 ))= [dt.month for dt in df7["Date" ]]"気温" ])'Month' )'temperature' )f'Nagasaki { target_year2} ' )0 ,35 ])1 ,12 ])
凝ったグラフを 3番目 (キャンバスの (2,1)要素)に追加してみましょう.
= fig.add_subplot(2 , 3 , 3 )= 1945 = df5[1 , 1 ) <= df5["Date" ])& (df5["Date" ] < datetime(target_year3 + 1 , 1 , 1 ))= [dt.month for dt in df8["Date" ]]"気温" ], "rd-" , label= f" { target_year} " )"気温" ], "b*:" , label= f" { target_year2} " )"気温" ], "g^:" , label= f" { target_year3} " )"Month" )"temperature" )f"Nagasaki { target_year} , { target_year2} and { target_year3} " )0 , 35 ])1 , 12 ])= "best" ) # 判例の位置をベストポジションに
箱ひげ図を書くこともできる.: boxplot
箱ひげ図を置く横軸目盛をpositionsで指定する
= fig.add_subplot(2 , 3 , 6 )"気温" ], positions= [1 ])"気温" ], positions= [2 ])"気温" ], positions= [3 ])"Year" )"temperature" )"boxcar plot" )0 , 35 ])0 , 4 ])f" { target_year} " , f" { target_year3} " , f" { target_year2} " ])
課題 k03
上記で紹介したリンク のページには,「日平均気温」の表が見えていますが, 「日平均気温」以外にも同様の形式のデータを選ぶことができます.
「降水量」の表をスクレイピングし,適切に表を整形し,指定した年の月別降水量の変化をグラフ表示する main() 関数を記述せよ.引数 years で対象の年を任意個並べた2次元 ndarray を受け取り,その配置通りにグラフ表示すること.また,以下の指示,および表示例に従って体裁も整えること.
グラフの縦軸である降水量の値の表示範囲は,全ての Axes 共通で,0から years に含まれる全ての年の最大降水量までとする.
例えば,以下のグラフでは,yearsは,1925年から20年おき6回の月別降水量を表示しているが,1945年の9月が表示対象の年で最高の降水量(約800mm)を記録している.したがって,すべてのグラフの縦軸の表示範囲は,0から約800mmとしている.
Figureの figsize は,(12,6) とすること.
いつものように,
> poetry new k03
> cd k03
> poetry add pandas matplotlib numpy lxml ipykernel
> poetry env use py
> code .でパッケージ開発の準備をする.
k03
┣─ src
│ └─ k03
│ └─ precipi_plot.py
└─ tests
└─ test_precipi_plot.pyの2つをコーディングする.
poetry sync を行なってからでないとテストできない.module not found: k03 となるであろう.
python では,あるファイル A から利用できる(参照できる)フォルダやファイルの場所が,
ファイル A と同じ階層
利用している python 環境(今回では,.venv にまとめられている)の site_packages フォルダの中
の2箇所に限定されている.
つまり, k03/src/k03/precipi_plot.py は tests/test_precipi_plot.py からは参照できない場所にある.
poetry sync を行うと,k03/src/k03フォルダ)を k03というパッケージ名で .venv の site_packages フォルダにリンクすることとなる.すなわち,そのpython環境であれば,どこからでも参照可能となる.
提出物は,いつものように whl ファイルであり,
> poetry version patch> poetry build によって,distsの下にできあがる.
課題の提出
以下の2ファイルをLACSで提出
poetry build でビルドした dist/k03-x.y.z-py3-none-any.whlファイルWord (.docx) または pdf のレポート (テスト実行画面のスクリーンショット画像と簡単な説明を含めること)
再提出のときは,poetry version patch してから再度ビルド
初回提出〆切: 6/25(水) , 最終提出〆切: 7/9(水)
10点になるまで再提出です.最終〆切を過ぎると1日毎に減点.
初回提出〆切は状況把握のためにあります.未完成であってもレポートで現状報告してください.